Leetcode : Search a 2D Matrix II

Problem statement

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

---

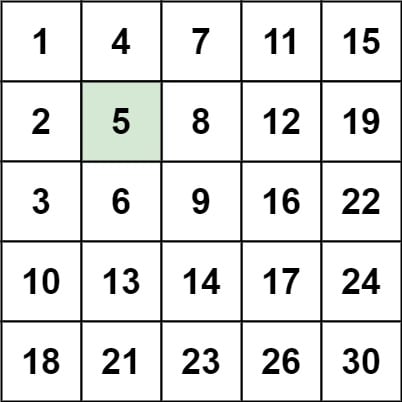
Example:1

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5

Output: true

Example:2

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20

Output: false

---

Constraints

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matix[i][j] <= 109
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• -109 <= target <= 109.

---

Link to the question on Leetcode

---

Idea

Bruteforce solution : The bruteforce solution for this problem is directly checking each cell of the matrix and return True if target is found or else return False.

Time complexity : O(M*N) , M = number of rows , n = number of columns.

---

Optimized solution for this problem is, as per the problem statement rows and columns are sorted from left to right and top to bottom , we can directly do binary search on each row.

Time complexity : O(M logN) , M = number of rows , n = number of columns.

---

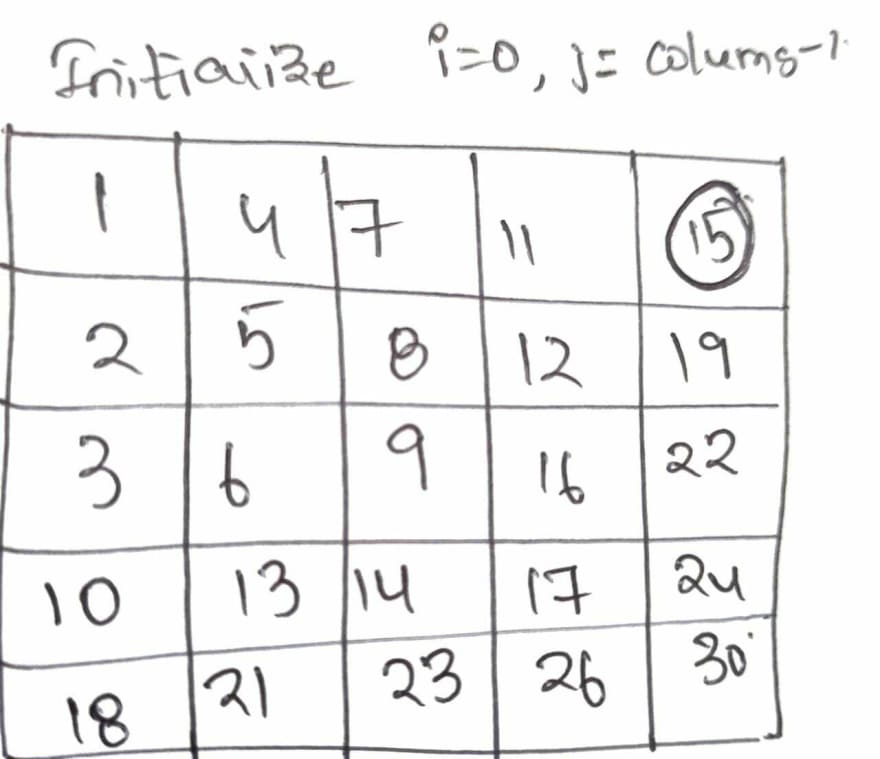
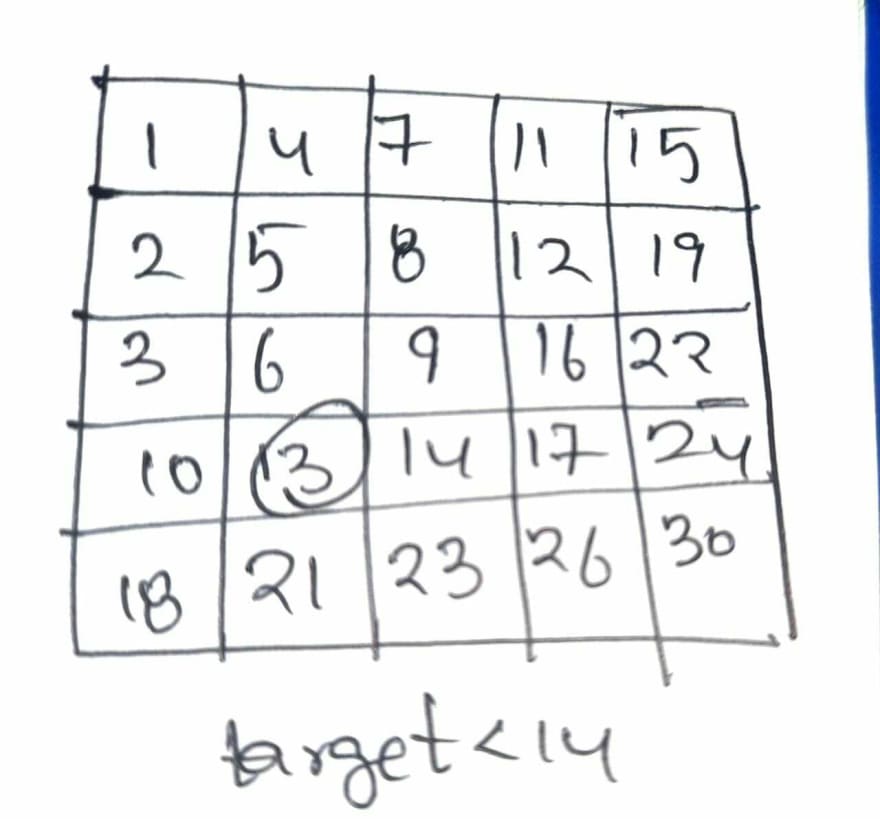
We can still optimize this solution to O(M+N).Lets discuss that solution with below example.

Lets initialize two variables i and j as first row and last column as below.

Since target is less the current cell we move to the left in the matrix (as rows and columns are sorted from left to right and top to bottom)

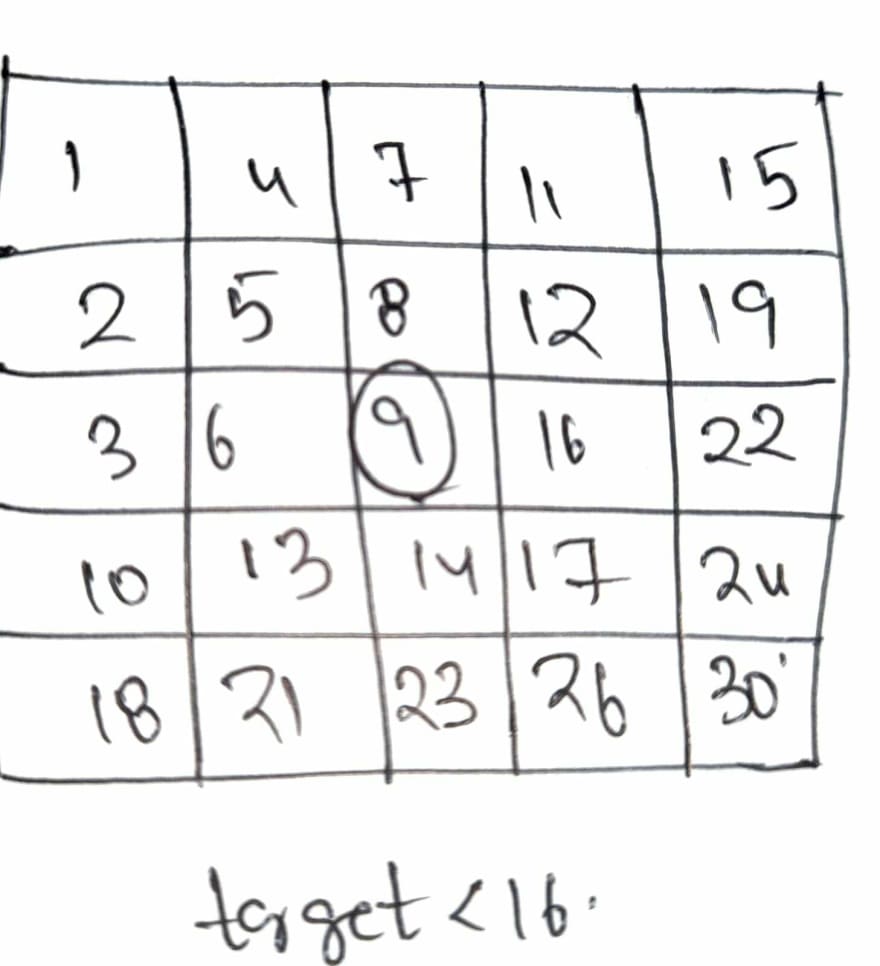
Since target is greater than current cell value we move to the next row.

Since target is still greater than the current cell value , we again move down the matrix.

Now target is less than the current cell value , so we move towards the left of the matrix within the current row.

Now target is greater than the current cell value , so we move down the matrix within the same column.

Now target is less than the current cell value , so we move to the left of the matrix within the current row.

At this point , we got cell whose value is equal to target , so we return True

So the overall idea here is whenever we encounter a cell whose value is greater than target we move towards the left within the same row having said that columns are sorted from top to bottom (so we are sure that we will not get the target element if move down the matrix , so we move to the left) and whenever we encounter a cell whose value is less than the target we move down the matrix as rows are sorted from left to right(as we can guarantee that moving left will not give us the target element).

Code - Python

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        rows = len(matrix)
        cols = len(matrix[0])
        i = 0
        j = cols-1
        while i >= 0 and j >= 0 and i < rows:
            cell_value = matrix[i][j]
            if cell_value == target:
                return True
            elif cell_value > target:
                j -= 1
            else:
                i += 1
        return False

---

Please like this post if you found this informative.