Introdução
Vamos retomar nossa jornada de explorar os fundamentos de estrutura de dados e algoritmos. Na última publicação, mencionei sobre o uso da técnica recursiva para o uso de um método de ordenação, e agora vamos nos aprofundar sobre recursão.
Essa série de publicações seguem meus estudos nesta disciplina de Estrutura de Dados do tecnólogo que estou fazendo, para acompanhar o que foi tratado até aqui, seguem os links das publicações anteriores.
- Explorando as Fundamentais Estruturas de Dados: Uma Introdução
- Explorando as Fundamentais Estruturas de Dados: Algoritmos de Ordenação
Vamos começar!
Entendendo a Recursão
Começando pelo começo, começar a usar recursão é difícil.
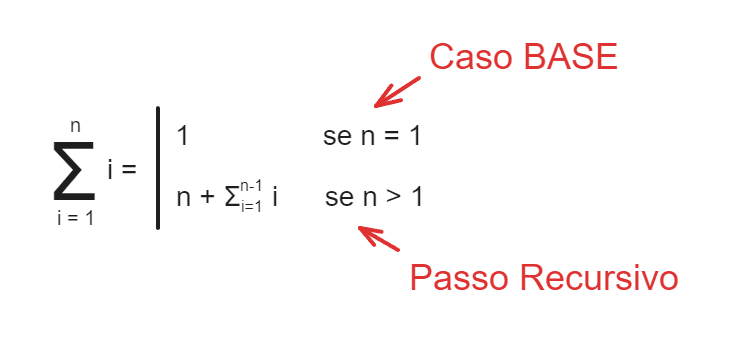
Uma forma de pensar sobre recursão é como se fosse uma função que chama ela mesmo até resolver um problema proposto. Isto envolver a utilização de um Caso BASE. E o caso base é o momento onde o problema é resolvido.
Explicando tudo isto, vamos para um dos exemplos mais comum a respeito de recursão, calcular o somatório de números inteiros positivos no intervalo de [1, n].
Aqui percebemos que uma função recursiva deve seguir duas regras fundamentais:
- Ter um Caso BASE (condição de parada) - se não a função realizará computação infinita
- Ter o Passo Recursivo (chamada recursiva) - onde a função chama a si mesmo, e sempre buscando resolver um problema quebrando-o em instâncias menores do que a chamada anterior.
Vamos começar a destrinchar essa recursão e entender essas etapas fundamentais.
A mecânica na técnica recursiva
Para fins de esclarecimento, o símbolo Σ (sigma) representa o somatório. Este símbolo, neste exemplo, significa que estamos fazendo repetidas somas dentro de um intervalo estabelecido, aqui, significa que ele vai de 1 até N.
Pseudocódigo
função Soma(N)
se N = 1 então
retorne 1
senão
retorne N + Soma(N-1)
fim se
fim função
Que pode equivaler a esta ideia
Então numa situação onde façamos o somatório até o número 5, seria o equivalente a dizer que
Java
public class SomatorioRecursivo {
public static int calcularSomatorio(int n) {
if (n == 1) {
return 1;
} else {
return n + calcularSomatorio(n - 1);
}
}
public static void main(String[] args) {
int N = 5;
int resultado = calcularSomatorio(N);
System.out.println("O somatório de 1 até " + N + " é: " + resultado);
}
}
Typescript
function calcularSomatorio(n: number): number {
if (n === 1) {
return 1;
} else {
return n + calcularSomatorio(n - 1);
}
}
const N = 5;
const resultado = calcularSomatorio(N);
console.log(`O somatório de 1 até ${N} é: ${resultado}`);
Praticando com Recursão
De posse deste conhecimento teórico até aqui, vamos praticar! Usualmente, costumo praticar o uso de técnicas e a melhora da minha capacidade de solucionar problemas com o site Codewars.
6 kyu - Mutual Recursion
Descrição do Problema
A Mutual Recursion nos permite aproveitar a diversão da recursão regular (onde uma função chama a si mesma até atingir uma condição de término) e aplicá-la a múltiplas funções que se chamam reciprocamente!
Vamos usar as sequências Feminina e Masculina de Hofstadter para demonstrar essa técnica. Você precisará criar duas funções, F e M, de forma que as seguintes equações sejam verdadeiras:
Exemplo
F(0) = 1
M(0) = 0
F(n) = n - M(F(n - 1))
M(n) = n - F(M(n - 1))
Solução
Aqui é bem simples, o problema nos dá o caso base e o passo recursivo então é só traduzir isto em código.
export function F(n:number):number {
if (n === 0) return 1;
return n - M(F(n-1));
}
export function M(n:number):number {
if (n === 0) return 0;
return n - F(M(n-1));
}
6 kyu - The Book of Mormon
Descrição
Os mórmons estão tentando encontrar novos seguidores e, para fazer isso, embarcam em missões.
Cada vez que eles vão em uma missão, cada mórmon converte um número fixo de pessoas (reach) em seguidores. Isso continua e todos os mórmons recém-convertidos, bem como todos os mórmons originais, embarcam em outra missão e convertem o mesmo número fixo de pessoas cada um. O processo continua até que eles alcancem um número predefinido de seguidores (target).
Os mórmons convertidos são únicos, de modo que não há duplicação entre eles.
Complete a função que calcula quantas missões os mórmons precisam embarcar para alcançar sua meta. Embora cada solução correta passe, para mais diversão, tente criar uma função recursiva.
Todas as entradas são inteiros positivos válidos.
Exemplo
starting_number = 10, reach = 3, target = 9 --> 0
# No missions needed because the number of followers already exceeds target
starting_number = 40, reach = 2, target = 120 --> 1
# Every mormon converts 2 people, so after 1 mission there are 40 + 80 = 120 mormons
starting_number = 20_000, reach = 2, target = 7_000_000_000 --> 12
# Mormons dominate the world after only 12 missions!
Solução
Diferentemente do primeiro desafio, aqui o problema nos apresenta situações que a partir da nossa interpretação devemos tirar nossas próprias conclusões para encontrar a solução.
A primeira coisa que conseguimos obter é o caso base e o caso mais importante, pois ele será a condição de parada para que nossa recursão não seja um loop infinito.
starting_number = 10, reach = 3, target = 9 --> 0
# No missions needed because the number of followers already exceeds target
Então quando startingNumber for maior que o target ele vai retornar 0.
Agora vamos ver os passos recursivos e como devemos chamar a função repetidamente para retornar o número de ciclos que a condição seja atingida.
starting_number = 40, reach = 2, target = 120 --> 1
# Every mormon converts 2 people, so after 1 mission there are 40 + 80 = 120 mormons
Ele faz uma verificação somando o número inicial (startingNumber) com o produto do número inicial vezes o alcance (reach), o que eu quero dizer é: 40 + (40 * 2).
Como no próximo ciclo, ele será igual ao target, ele retorna 1. E importante, que agora nós obtemos mais uma informação do Caso BASE, é que não basta ser só maior, tem que ser maior ou igual.
Então para cada ciclo de conversão soma-se 1.
Vamos a solução que eu encontrei para este problema:
export function Mormons(startingNumber:number, reach:number, target:number):number{
if (startingNumber >= target) return 0;
return 1 + Mormons(startingNumber + startingNumber * reach, reach, target);
}
Considerações Importantes sobre Recursão
É importante considerar sempre com muito cuidado a condição de parada, ou seja, o processo que as chamadas deverão ser interrompidas.
A recursão não obrigatoriamente traz economia de memória, afinal, os valores que são mantidos em pilhas para cada etapa em que são processados (leia sobre stack overflow).
Stack Overflow: É um efeito adverso de uma recursão mal elaborada. A função recursiva chama a si mesmo repetidamente sem encontrar um ponto de parada até que não haja mais espaço disponível em memória.
Nem sempre será mais rápido, justamente por conta do motivo acima citado.
Conclusão
Chegamos ao fim de mais um capítulo nesta série sobre Estruturas de Dados e Algoritmos, e encontramos nessa técnica uma maneira de solucionar problemas de forma elegante e modular.
Em contrapartida, mais importante do que ser uma forma elegante é a sua importância quando formos estudar estruturas de dados como as árvores, onde entender recursão é essencial para esta etapa do aprendizado e do conhecimento.
Até a próxima!
Sobre o Autor
Meu gosto pela escrita se entrelaça com a vontade de compartilhar o que estou aprendendo ao longo desse percurso. Acredito que cada artigo é uma oportunidade não apenas de solidificar meu conhecimento, mas também de oferecer insights valiosos a outros aprendizes.
Minha esperança é que essas contribuições não apenas auxiliem quem busca conhecimento, mas também me impulsionem na busca por novas oportunidades e desafios na indústria de desenvolvimento de software.









Top comments (0)