Decoding the beauty of cryptography :

What is cryptography :

Cryptography is a practice and study of techniques for securing communication between two hosts . Which ensures that no middle person can understand the communication going on between two hosts .

Process of cryptography :

History of encryption :

• The Caesar cipher is one of the earliest known and simplest ciphers . It is a type of substitution cipher in which each letter in the plaintext is 'shifted' a certain number of places down the alphabet .
  

• Enigma cipher :
  The enigma cipher is a field cipher used by Germans during the world war 2.
  

---------------------------------------
Encryption : key values a = 17 , b = 20
---------------------------------------

original text : t  w  e n  t  y     f i f t  e  e  n
            X : 19 22 4 13 19 24    5 6 5 19 4  4  13
ax + b % 26   : 5  4  10 7 5  12    1 0 1 5  10 10 7
Encrypted text: f  e  k  h f  m     b a b f  k  k  h

------------------------- 
Decryption : a^n - 1 = 23
-------------------------

Encrypted Text      : f  e  k  h f  m     b a b f  k  k  h
Encrypted Value     : 5  4  10 7 5  12    1 0 1 5  10 10 7
23 * (X - b) mod 26 : 19 22 4 13 19 24    5 6 5 19 4  4  13
Decrypted Text      : t  w  e n  t  y     f i f t  e  e  n 

• Digital encryption standards : The digital encryption standard (DES) is a symmetric key block cipher published by NIST . DES is an implementation of Feistel cipher .

Classification of cryptography :

1. Symmetric key cryptography (secret key encryption)
2. Asymmetric key cryptography (public key encryption)

Symmetric key cryptography is further divided into two parts

A. classical Cryptography :

• Transposition cipher
• substitution cipher

B. Modern Cryptography :

• Stream cipher
• Block cipher

Symmetric key cryptography :
An encryption system in which the sender and receiver of a message share a single common key that is used to encrypt and decrypt the message . The most popular symmetric key system is the data encryption standards(DES) .

Classical cryptography :

1. Transposition cipher : In this kind of encryption the positions held by units of plaintext (which are commonly characters or group of characters) are shifted according to the regular system so that the ciphertext constitutes a permutation of the plain text .

1 2 3 4 5 6    4 2 1 6 3 5
m e e t m e    t e m e e m
a f t e r p    e f a p t r
a r t y        y r a t

plain text  : meet me after party 
key used    : 421635
cipher text : temeemefaptryrat

1. substitution cipher : Methods of encryption by which units of plain text area replaced with cipher text , according to a fixed system the "units" may be single letters, mixtures of the above , and so forth .

A B C D E F G H I J K L M     RTO13 is a caesar cipher , a type of 
| | | | | | | | | | | | |     substitution cipher in RTO13 
N O P Q R S T U V W X Y Z     alphabet is rotated 13 times .

plain text : ABCDEFGHIJKLMONPQRSTUVWXYZ
keyword    : ZEBRAS
cipher text: ZEBRASCDFGHUKLMNOPQTUVWXY

Modern Cryptography :

1. Stream cipher :
   A symmetric or secret-key encryption algorithm that encrypt a single bit at a time . with a stream cipher , the same plaintext bit or byte will encrypt to a different bit or byte every time it is encrypted .
   

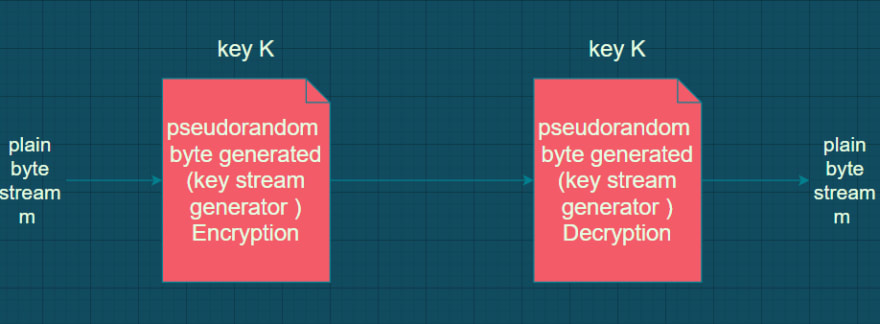
2. Block cipher :
   The alternative method is block cipher in which a key and algorithm are applied to block of data rather than individual bits in a stream .

Asymmetric key encryption :

It usages a pair of keys public key which can be disseminated widely over the network and private key is only know to the host .

Some examples of Asymmetric key :

• Diffie-Hellman key exchange
• DSS
• RSA

Diffie-Hellman key exchange
It is also known as exponential key exchange is a method of digital encryption that uses numbers raised to specific powers to produce decryption keys on the basis of components that are never directly transmitted , making the task of a would-be code breaker mathematically overwhelming .

Working of Diffie-Hellman :

step-1 :

• Assume a prime number and selecting its primitive root .
• Assume a prime number q .
• select alpha primitive root of q (alpha < q)
• alpha is a primitive root of q if :

alpha mod q , aplpha ^ 2 mod q .......... alpha ^ q-1 mod q
is implies 1, 2, 3, ..... q-1

step-2 :
Finding private key and public key of sender and receiver .

Assume xa (private key of user a)   |
----------                          |
| xa < q |                          |
----------                          |    (Sender)
Now , calculate public key ya       |
------------------------            |
|ya = alpha ^ xa mod q |            |
------------------------
Assume xb (private key of user a)   |
----------                          |
| xb < q |
----------
                                    |    (receiver)
Now , calculate public key , yb
----------------------
| yb = alpha^xb mod q |             |
-----------------------
                                    |
__Step-3 :__
Generate secret key at senders and receiver's side so sender has his private key         = xa
    receiver public key = yb
    prime number        = q

key is being generated with the following formula :
------------------
| K = yb ^ mod q |
------------------
similarly receiver has his private key = xb
                           receiver public key = ya
                           prime number = q 
* key is being generated :
-------------------
| K = ya ^ xb mod q |
--------------------
* After calculating the key on both the sides 
K = yb ^ xb mod q   ==  K = yb ^ xa mod q

There are lot more to know :

• prefer old friend wikipedia for in-depth knowledge .

• And cryptii for practice .

prefer site for practice

Thanks for reading 👨‍💻👨‍💻👨‍💻