TL;DR In this article we will take a look at state machines and how they are applied to model business processes, and a particular library implementing that for Elixir and Ecto.
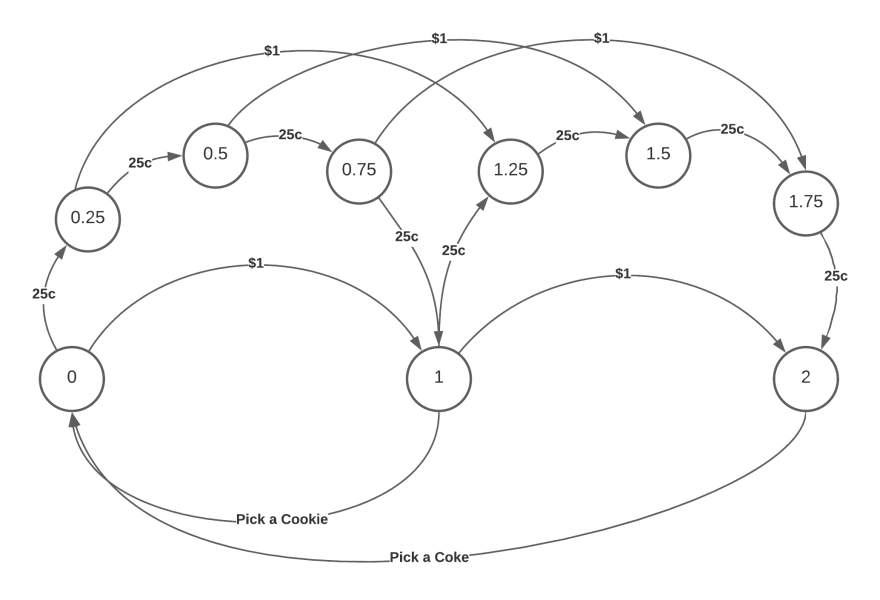
Let's think about vending machine. Its operation defined by some set of constraints. Can you get a Coke when there are no bills in? No. Would it change if you put a dollar in there, while the beverage price is $2? Still no, duh. All of these properties combined constitute a State. Think of a State as a slice of the space-time continuum in the microcosm of this particular vending machine.
In this case, there is nothing but current balance accounted in the state, but in reality there is gonna be a whole lot more of variables there. Is supply of cokes and cookies unlimited? Unlikely! Should we consider the process of dispensing a state? Probably, since it's not momentary and we don't want any events to be allowed until the machine reports that the dispensing is over. But let's focus on money for now, it is gonna get whole lot more complicated when we start accepting coins. Watch what happens should we just add quarters:
See? Modeling a real life business process with pure finite state automata would be insanely complicated. Instead we can reduce the notion of state to a tag, a conventional name of a group of states. Are we collecting bills or coins, let’s call it collecting. Are we dispensing merchandize? Well, you see where this is going. We will still maintain internal variables that can be arbitrarily complicated, but now rather consider a mode of operation of the machine as a state, and not every possible combination of those variables.
This allows us to reduce this state machine to only two states including dispensing. Let's generalize the diagram and introduce the language:
Circles are States, as you might have guessed already. Arrows and everything that happens along the way are Transitions. Rectangles are Callbacks or actions that mutate variables of the inner state at some moments in life cycle. The rhombus is a Guard, a condition that has to be met to proceed with transition. Finally, an Event — an external signal accompanied with an optional value that triggers the transition. This diagram is a bit verbose, but when it's written using DSL or plain english, it's very simple:
- When in
collectingonput X, add X to balance, then move tocollecting - When in
collectingonget ITEM, if balance >= ITEM.price, then move todispensing - When in
dispensingondone, subtract item.price from balance, then move tocollecting
So far, we have defined the following:
- Two states
collectinganddispensing - Three events
put X,get ITEM,done - One guard on
get ITEMevent:balance >= ITEM.price - Two callbacks:
balance + Xonput X, andbalance - ITEM.priceondone
The internal state consists of 2 variables: balance and item; the latter is set on moving to dispensing and cleared afterwards. Actually, these are also callbacks, but they're missing in the diagram above. Well, modeling is not easy and we normally revisit the schema many times afterwards.
State Machine in Elixir
Modeling the same State Machine in Elixir with state_machine is straightforward. I added one extra event to be able to fulfill the merchandize and omitted the implementation of callbacks and guards for now:
defmodule VendingMachine do
alias VendingMachine, as: VM
use StateMachine
defstruct state: :collecting,
balance: 0,
merch: %{},
dispensing: nil
defmachine field: :state do
state :collecting
state :dispensing
event :deposit, after: &VM.deposit/2 do
transition from: :collecting, to: :collecting
end
event :buy, if: &VM.can_sell?/2, after: &VM.reserve/2 do
transition from: :collecting, to: :dispensing
end
event :done, after: &VM.charge/1 do
transition from: :dispensing, to: :collecting
end
event :fulfill, after: &VM.fulfill/2 do
transition from: :collecting, to: :collecting
end
end
end
A cool feature here is that if you mistype the state name in transition, it'll be caught at compile time. The definition is getting verified. It might seem useless when we have just two states, but in larger state machines it can be life saving.
Now let's take a look at callbacks:
def deposit(%{balance: balance} = model, %{payload: x})
when is_integer(x) and x > 0
do
{:ok, %{model | balance: balance + x}}
end
def deposit(_, _) do
{:error, "Expecting some positive amount of money to be deposited"}
end
Callbacks can be of arity 0, 1 and 2. Zero arity callback would just produce some side effects independent of the state. The first argument passed into callback is the model itself. The second is the context, a structure containing the metadata supporting the current transition. This includes event payload, info about transition, such as old and new states, and a link to the state machine definition.
Return value of each callback is structurally analyzed on runtime in order to determine the appropriate action. You can return {:error, error}, and this will disrupt the transition and return {:error, {callsite, error}} in the very end. Here the callsite is pretty much the moment when the callback is triggered (after_event, for example).
If you return {:ok, updated_context}, it will update the current context. This is hardcore, but you can do that. More often you might want to update the model only. To do that, return {:ok, updated_model} and it'll be replaced in the context.
One important caveat is that currently only fully qualified function captures (&Module.fun/arity) are supported in callbacks. In future versions it will support lambdas and possibly local functions and atoms.
Next is a Guard can_sell?:
def can_sell?(model, %{payload: item}) do
model.merch[item]
&& model.merch[item][:available] > 0
&& model.merch[item][:price] <= model.balance
end
First we make sure that the item is present in the inventory as a class, then we check if it is currently available, finally we make sure that balance is enough. There's one important point to note. Due to the mechanics of state_machine, guards do not leave any trace; they run sequentially while it's trying to find matching transition, as there can be many possible paths. In other words, for the user it will appear as if the event was impossible, and by using introspection tools you can find that out in advance, by checking allowed_events for a particular model.
The rest of callbacks should look trivial:
def reserve(model, %{payload: item}) do
{:ok, %{model | dispensing: item}}
end
def charge(%{balance: balance, dispensing: item, merch: merch} = model) do
{:ok, %{model |
balance: balance - merch[item][:price],
merch: put_in(merch[item][:available], merch[item][:available] - 1),
dispensing: nil
}}
end
def fulfill(%{merch: merch} = model, %{payload: additions})
when is_map(additions)
do
{:ok, %{model |
merch: Map.merge(merch, additions, fn _, existing, new ->
%{new | available: new.available + existing.available}
end)
}}
end
It's time to play with it. I created a little repo for this sample project so everybody could clone and try it locally. However I'll just post the test sequence here, it should be self explanatory:
alias VendingMachine, as: VM
vm = %VM{}
# Let's try to load it with some coke and cookies
assert {:ok, vm} = VM.trigger(vm, :fulfill, %{
coke: %{price: 2, available: 1},
cookie: %{price: 1, available: 5}
})
# And one more coke to ensure correct merging
assert {:ok, vm} = VM.trigger(vm, :fulfill, %{
coke: %{price: 2, available: 1},
})
assert vm.merch.coke.price == 2
assert vm.merch.coke.available == 2
assert vm.merch.cookie.price == 1
assert vm.merch.cookie.available == 5
# Now let's grab a coke
assert {:error, {:transition, _}} = VM.trigger(vm, :buy, :coke)
# But wait, we could actually tell that before even trying:
refute :buy in VM.allowed_events(vm)
# Oh right, no money in there yet
assert {:ok, vm} = VM.trigger(vm, :deposit, 1)
assert {:ok, vm} = VM.trigger(vm, :deposit, 1)
assert vm.balance == 2
# Huh, hacking much? Note how error carries the callsite where it occurred
assert {:error, {:after_event, error}} = VM.trigger(vm, :deposit, -10)
assert error == "Expecting some positive amount of money to be deposited"
# Gimme my coke already
assert {:ok, vm} = VM.trigger(vm, :buy, :coke)
assert vm.state == :dispensing
# While it's busy, can I maybe ask for a cookie, since the balance is still there?
assert {:error, {:transition, "Couldn't resolve transition"}} = VM.trigger(vm, :buy, :cookie)
# Okay, the can is rolling into the tray, crosses the optical sensor, and it reports to VM...
assert {:ok, vm} = VM.trigger(vm, :done)
assert vm.state == :collecting
assert vm.balance == 0
assert vm.merch.coke.available == 1
When we use defmachine macro in the VendingMachine module, it creates some auxiliary functions. The most important one is trigger(model, event, payload); when it is called, it attempts to run an event. This function returns {:ok, updated_model} if the transition worked or {:error, {callsite, error}} if it didn't. By checking callsite, you can find out where it was rejected.
StateMachine supports Ecto out of the box, by wrapping triggers in transactions and calling Repo.update() on the state field, but it requires a bit of configuration. It can also work as a process by automatically generating GenStatem definition. More on that in the next posts.
Links:









Top comments (0)