Problem statement
Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.
Note that you need to maximize the answer before taking the mod and not after taking it.
Link to the question on Leetcode
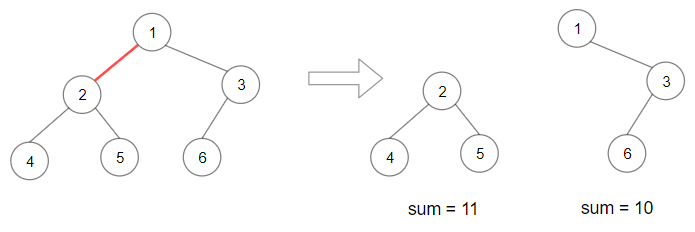
Example:1
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Approach
The question says that we have to split the binary tree to sub tree where the product of sum of two subtrees are maximized. Splitting the binary tree means removing one edge from binary tree.
We can solve this problem by pre calculating the sum of subtree for each node which will help us in finding the maximum product of sum of sub trees.
So the idea here is we have to find out the maximum value of subtree multiplied with total tree sum minus subtree sum which gives the product of sum of subtrees.
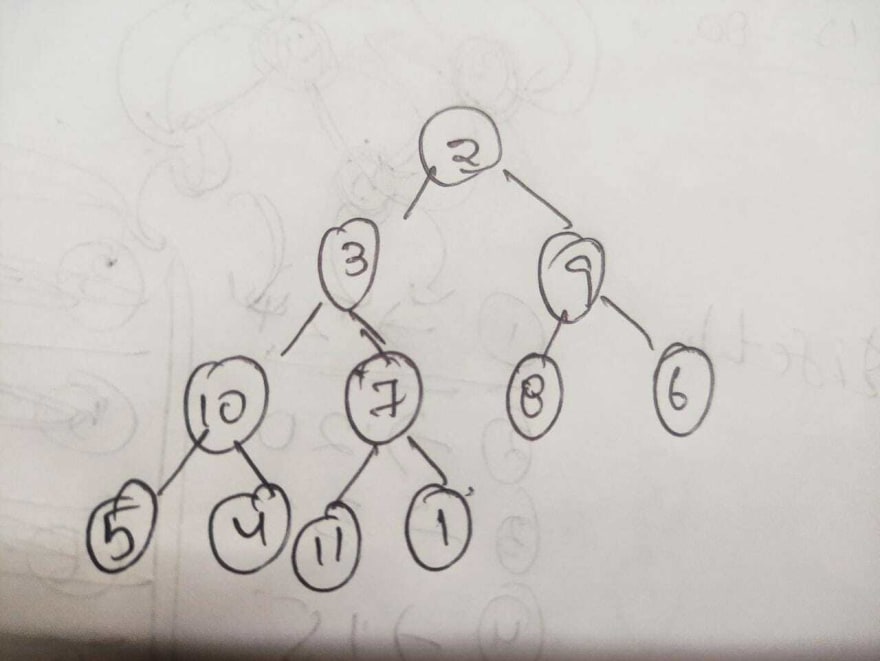
Lets solve this with example [2,3,9,10,7,8,6,5,4,11,1]. This is the given tree. Below is the tree representation of above input.
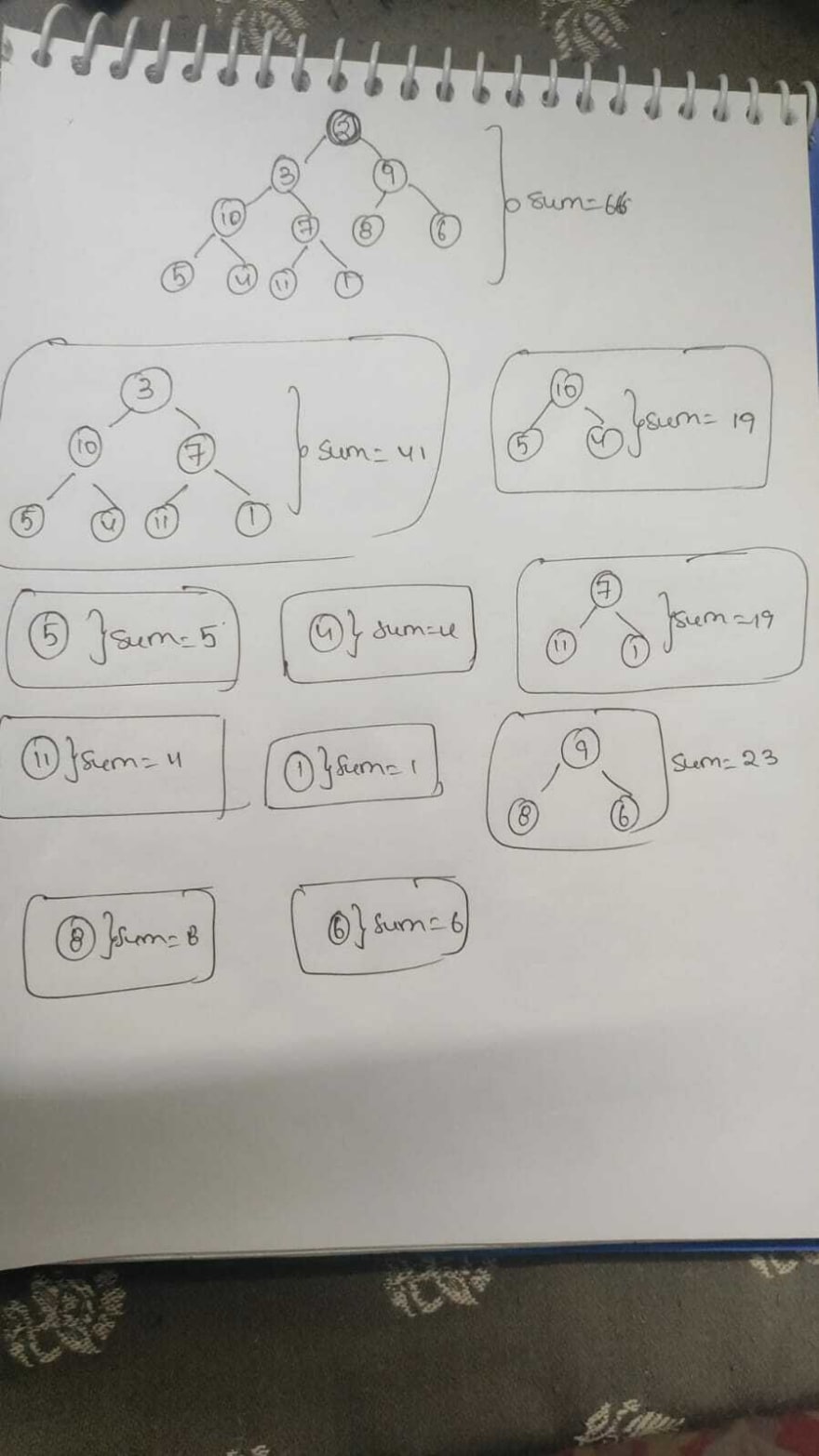
First lets calculate the sum of subtree for each node. Sum of all the subtrees are as below:
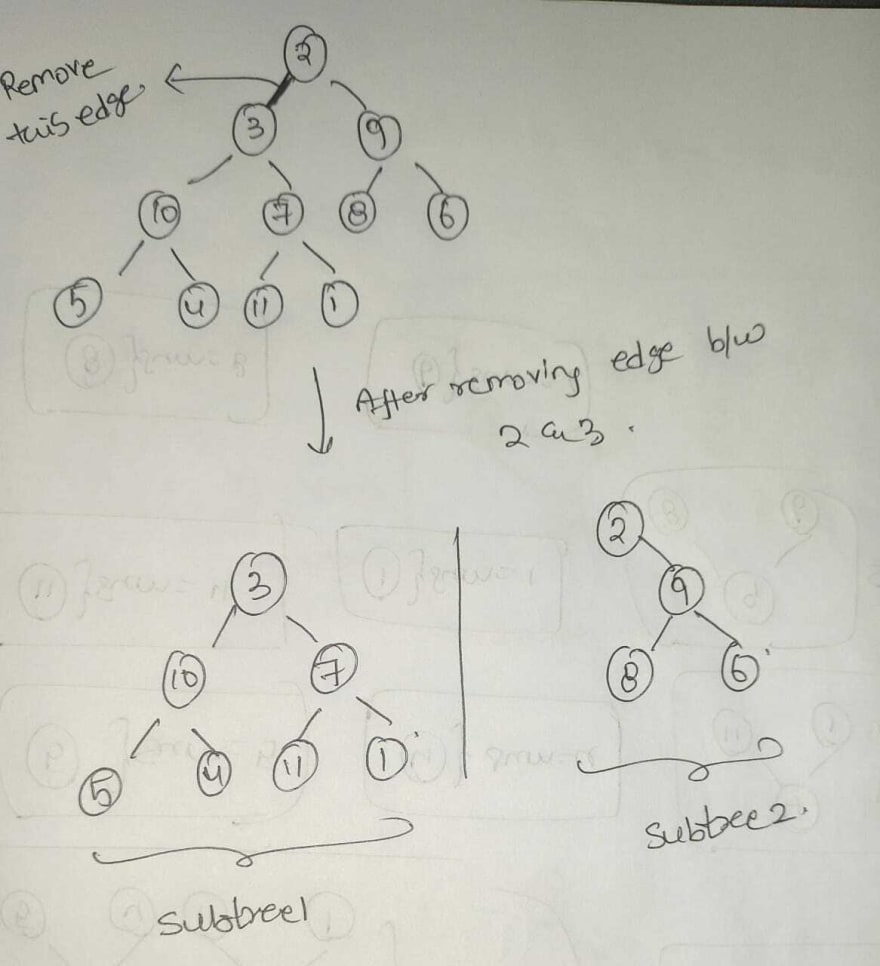
Now lets try to remove the edge between root node "2" and its left child "3" , we get two subtrees . we can get the sum of two subtrees directly from our pre calculated values . The sum of two subtrees can be calculated as in below image.
We can directly get the sum of subtree1 from our pre calculated values and sum of other subtree will total tree sum minus subtree1 sum. Find the product of these two subtrees.
In the same way we have to try removing all the edges one by one and find the maximum product of sum of subtrees.
Note:To pre calculate all the subtrees sum use post order traversal of binary tree and store all the values in a dictionary.
Code
import math
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxProduct(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
subtree_sum = dict()
self.subtree_sum(root,subtree_sum)
root_subtree_sum = subtree_sum[root]
maximum = 0
for subtree in subtree_sum:
maximum = max(maximum , subtree_sum[subtree] * (root_subtree_sum - subtree_sum[subtree]))
return int(maximum%(math.pow(10,9)+7))
def subtree_sum(self,root,subtree_sum):
if root is None:
return
self.subtree_sum(root.left,subtree_sum)
self.subtree_sum(root.right,subtree_sum)
left_sum = 0
right_sum = 0
if root.left:
left_sum = subtree_sum.get(root.left)
if root.right:
right_sum = subtree_sum.get(root.right)
subtree_sum[root] = left_sum + right_sum + root.val




Top comments (0)