Introduction
One of the first steps a compiler must take is parse the human-readable program format, usually a plain text file, and put it into a structure the compiler can work with; the Abstract Syntax Tree (abbreviated to AST).
Here's a simple example with code followed by an AST:
f 2
and a slightly more complex example:
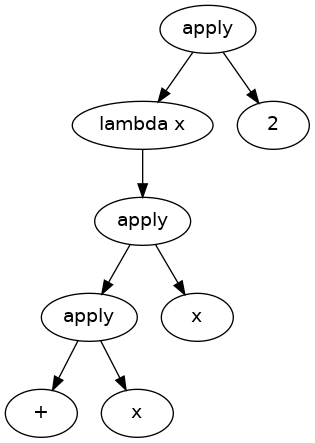
( \x -> x + x ) 2
in this post I wish to define the AST for my language based on requirements set forth previously.
Underlying litterature
I'm primarily basing myself on the following work:
[Peyton Jones & Lester 1992] Implementing Functional Languages: a tutorial. The title of this book is self-explanatory, though I should mention it covers lazy languages specifically.
[Martin-Löf 1973] An intuitionistic theory of types: predicative part. This article first describes the Martin-Löf type system, that is, dependent types. It explains how propositions about values in a program can be expressed themselves as types and terms.
[Atkey 2018] Syntax and Semantics of Quantitative Type Theory. This article describes quantitative type theory, which marries dependent types with linear values and erasure.
Of course, I'm also using a lot of transitive knowledge and things I picked up here and there, but have no specific source for.
A default AST
To define how an AST might look, we must specify a language grammar. This is often done using BNF (Backus-Naur Form) notation. In languages like Haskell and Idris it is incredibly easy to express it directly in a type, so I will do that instead.
I start from the AST given in [Peyton Jones & Lester 1992] p.17, translated to Idris:
data Expr a
= EVar String
| ENum Int
| ECtr Int Int
| EAp (Expr a) (Expr a)
| ELet IsRec (List (a, Expr a)) (Expr a)
| ECase (Expr a) (List (Alt a))
| ELam (List a) (Expr a)
data Alt a = (Int, List a, Expr a)
Here, the type-variable a is the "binder" of values. Generally this will be a String representing the name of a variable, but different types could be used as well.
EVar represents named variables, such as x.
ENum is for number primitives: 1, 2, 42, etc.
ECtr is less intuitive, when we define a type, such as data MaybeInt = Just Int | Nothing, each constructor can be given a number, called the tag. The tag can be used internally by case expressions to match on the right constructor. The other Int argument to ECtr is the arity: how many arguments the constructor takes. In the example Just has arity 1 and Nothing has arity 0.
EAp is function application. For instance, f x would parse to EAp (EVar "f") (EVar "x").
ELet is for let ... in expressions, where the (a, Expr a) values are the variable definitions.
ECase is a case expression. The Alt a type has a tag value to match, with a list of constructor arguments, and an expression.
ELam is for lambda functions.
There are a few changes I wish to make based mostly on preference.
First, we can determine whether a let-expression is recursive, e.g. let xs = 1 : xs in ..., by static analysis of the enclosed definitions. [Peyton Jones & Lester 1992] does this, more or less, in 6.8.3. I prefer not to have a specific field for it so that I have a single source of truth. I will remove the IsRec field. I suspect the book only uses this field to avoid having to explain dependency analysis first.
Second, numbers are just constructors that should really check their priviledge. Defaulting to int is a fantastic source of bugs. By giving numbers special treatment we are also overlooking more generic optimizations. ENum goes.
Third, I'm taking a hint from Elm style guidelines and replacing builtin types by more meaningful custom ones.
After those basic changes we are left with:
data Expr a
= EVar VarID
| ECtr CtrID
| EAp (Expr a) (Expr a)
| ELet (List (Def a)) (Expr a)
| ECase (Expr a) (List (Alt a))
| ELam (List a) (Expr a)
data Alt a = MkAlt CtrID (List VarID) (Expr a)
data Def a = MkDef a (Expr a)
I have left the various IDs intentionally undefined.
Making the AST hollistic
To consider what changes are necessary to support hollistic programming, we must go back to the language's goals.
If we wish to define the whole system in a language, rather than one particular program, we must start considering changes in code over time. Typically, it is the responsibility of the developer to ensure that changes to not break compatibility with persistent systems, such as databases. If such systems are generated by the compiler, it is the compiler that must be able to prove compatibility with some previous version. Immutability helps a great deal here. Just as Elm uses immutability to quickly determine what areas of a DOM need updating, so too we wish to have immutability in program definitions themselves, so we can correctly determine what is compatible. It would be nice if we had some kind of "metapurity": make the act of programming itself pure.
To achieve this, I will copy the identify-by-hash approach of unison. Where names are stateful and may point to different functions over time, hashes are stateless. If a function changes, so does its hash.
Of course, programming with hashes directly is infeasible for programmers. We need a human-compatible language, let's call it the display language. In most other programming languages, the display language is the source of truth. The core language AST is derived from it during compilation. There is a missed opportunity here.
A lot of effort is being wasted by developers fighting about pure display concerns: tabs vs spaces, camelCase vs PascalCase vs snake_case vs kebab-case, operators vs functions, import definitions, naming, alignment, egyptian brackets... after removing names as identifiers, none of these concerns change a program's AST in the core language. If we make the core language the source of truth, and define the display language as (isomorphic to) the core language plus some display information (e.g. variable names), we can do away with those issues entirely.
Now, back to the AST
Many naming issues are already resolved by resorting to hashes, but variables may also be bound by let-expressions, lambdas, and supercombinators. For there, we don't really need hashes. We can use a de Bruijn index, slightly adapted to work with let-expressions and supercombinators as well (both can be converted to lambda functions, but that seems counter-productive).
I will have to distinguish between local variables, using de Bruijn indices, and global variables. Binder types have become superfluous, we just need to know how many binders a binding-expression has.
data Expr
= ELVar Nat ||| de Bruijn index of locally-bound variable
| EGVar Hash ||| Hash of globally bound supercombinator
| ECtr CtrID
| EAp Expr Expr
| ELet (List Expr) Expr ||| 1st arg is definitions, second is the "in" part
| ECase Expr (List Alt)
| ELam Nat (Expr a) ||| Only need to know number of arguments
data Alt = MkAlt CtrID Expr ||| # arguments derived from CtrID
Dependent typing
This leaves us with 2 problems: CtrID is not defined, and we are missing a way to use types as values.
unfortunately, I start using math heavily here, and have not found a satisfactory way to display it on dev.to that does not require a lot of manual work. I ask you to continue reading on my website instead.







Top comments (0)